Reading notes: unsupervised word translation
I actually have a similar idea at the beginning of this year, using GAN to push word embeddings of two different languages to the same space, and see if we can learn word translation.
I tried a toy task, which is training two different embeddings given the same English corpus. This is simple because every word has an exact correspondence which is itself. And also it’s easy to evaluate. However, I failed. Thus I gave up on this project and in the first half of this year, several papers have been released applying similar idea.
The paper introducing here is by far the best unsupervised word translation method. It can even beat the supervised learning method some times. And their method doesn’t use any parallel data (even when you do validation).
Method
Supervised method (Preliminary knowledge)
In the supervised setting, we assume we already have the word embeddings of two languages, and also we have a dictionary including n word translation pairs. We can use these pairs as anchor points and learn a mapping so that the two embeddings are aligned.
In [1], we suppose the embeddings of the words in the pairs are \(\{x_i,y_i\}_{i \in [1,n]}\); now we learn a linear mapping \(W\) to transform the embedding space of one language to another language. The \(W\) is learned to minimize the pairwise euclidean distances after mapping:
\[$W^* = {\arg\min}_{W} \|WX-Y\|_F\]\(X\) and \(Y\) are $d\times n$ matrices which corresponding to the dictionary, and \(W\) is a \(d\times d\) matrix.
After we get this \(W\), for any word \(s\) which is not in the dictionary, we can find its nearest neighbor in the other language as its translation.
\[t = \arg\max_t cos(Wx_s, y_t)\]Based on this method, [2] add the constraint that \(W\) has to be orthogonal. So the problem now is actually known as Procrustes problem. We can SVD \(YX^T\) to get closed form solution:
\[W^* = {\arg\min}_{W\in O_d(\mathbb R)} \|WX-Y\|_F = UV^T, \text{with}\ U\Sigma V^T = \text{SVD}(YX^T)\]Above is the method when you have dictionary. What should we do if we don’t have dictionary? The method proposed in this paper is as follows:
- Learn a \(W\) using GAN which pushed the embeddings space close enough so that the discriminator can not tell them apart.
- Use this \(W\) to find some word pairs that the model is confident about, treat them as ground truth dictionary, and refine the \(W\) using Procrustes method.
- Use dubbed CSLS as distance metric to do nearest neighbor search.
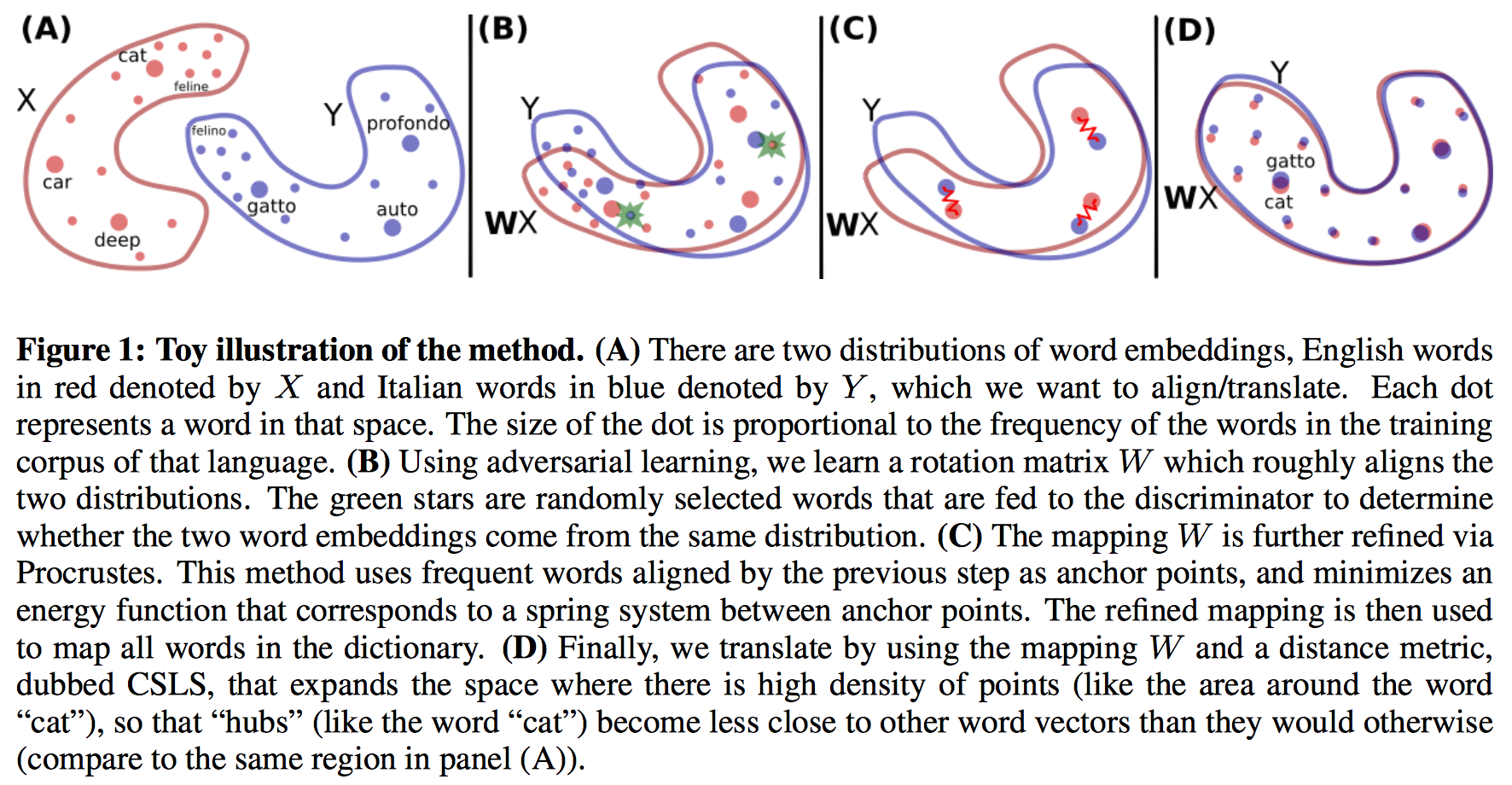
Algorithm pipeline
GAN training
It’s quite intuitive to apply GAN. We learn a discriminator to distinguish from \(WX\) and \(Y\), and we update \(W\) to fool the discriminator.
Discriminator objective:
\[L_D(\theta_D| W) = -\frac{1}{n}\sum_{i=1}^n \log P_{\theta_D}(\text{source}=1|Wx_i) - \frac{1}{m}\sum_{i=1}^m \log P_{\theta_D}(\text{source}=0 | y_i)\]Generator(Mapping) objective:
\[L_D(W|\theta_D) = -\frac{1}{n}\sum_{i=1}^n \log P_{\theta_D}(\text{source}=0|Wx_i) - \frac{1}{m}\sum_{i=1}^m \log P_{\theta_D}(\text{source}=1 | y_i)\]Because some words are rare, so the embeddings learned are worse because of less update during training. It’s a hard time for GAN to align these words. If we include these words, it will harm the GAN training.
Thus, when training discriminator, the authors only use the most frequent 50000 words for each language (In total, when training generator, 200k most frequent word are used). During training, words are uniformly sampled from these 50k words. (Sampling by frequency achieves no gain)
When training \(W\), to assure that W is orthogonal (orthogonality provides euclidean distance invariance and also help training stability), the author uses a special update rule:
\[W \leftarrow (1+\beta)W-\beta(WW^T)W\]\(W\) updated in this way is close to be orthogonal. (\(\beta\) is chosen to be 0.01)
Refine using Procrustes
Here we hope we can extract some high-quality translation pairs from learned \(W\), and use them as anchor points to get better \(W\) by Procrustes.
Their method is, find the nearest neighbor(in the other language) of each word. If a pair of words are mutual nearest neighbors, then we add them into the dictionary and regard them as high-quality translation.
Using these high-quality translations, we can refine our \(W\).
Nearest neighbor
The problem left is how to find the nearest neighbors.
NN is assymmetric; y is the nearest neighbor of x doesn’t mean x is also y’s. In high-dimension space, there’s a known phenomenon called hubness. Some points (called as hubness) can be the nearest neighbor of multiple points, however some poitns (called anti-hubness) is not nearest neighbor of any points.
In this paper, they propose a cross-domain similarity local scaling (CSLS) method, so that there are more mutual nearest neighbor pairs.
The method is like this: for each word, we can find the K nearest neighbors in the other language (by cosine similarity and \(W\)), denoted as \(\mathcal N_T(s)\) and \(\mathcal N_S(t)\).
Then we define CSLS:
\[CSLS(s,t) = 2cos(Wx_s, y_t) - r_T(s) - r_S(t)\]CSLS measure the similarity between two words (from different language). We can see that, only \(Wx_s\) and \(y_t\) being close is not enough, the similarity will also be penalized by the hubness of \(s\) and \(t\). This prevent that some word can be the nearest neighbor of multiple words.
validation criterion
Another novelty of this paper is they propose a validation criterion for model selection and early stopping.
Some paper will use labeled data for validation, and choose the hyperparameter or early stop according to the validation result. The problem is, in this way it’s implicitly fitting the labeled data in some way.
The criterion proposed in this paper is: pick the 10k most frequent words from source domain, find their nearest neighbor according to CSLS, and calculate the mean cosine distance of these 10k pairs. They found the criterion is correlated with word translation accuracy, so later they use this for hyperparameter tuning and early stopping.
##Experiment Since CSLS is only a distance metric, it can be also applied to supervised method. We can see that CSLS can improve both supervised and unsupervised method compared to naive nearest neighbor. And there is only one hyperparameter K to choose for CSLS, and they found choosing K to be 5, 10, 50 doesn’t affect the result.
pretrained embedding: the authors both cbow embedding and fasttext embedding and fasttext is significantly better.
refinement: After GAN training, the model can do reasonably well but still worse than supervised method. However, after using refinement, the model can be closer or even beats supervised method.
##Conclusion It’s actually trivial to use the idea of GAN, however, it’s more important how to make things work.
[1] Mikolov, Tomas, Quoc V. Le, and Ilya Sutskever. “Exploiting similarities among languages for machine translation.” arXiv preprint arXiv:1309.4168 (2013).
[2] Xing, Chao, et al. “Normalized Word Embedding and Orthogonal Transform for Bilingual Word Translation.” HLT-NAACL. 2015.